dackdive's blog

新米webエンジニアによる技術ブログ。JavaScript(React), Salesforce, Python など

「みんなのデータ構造」学習メモ：2.1 ArrayStack

書籍 データ構造とアルゴリズム

「みんなのデータ構造」という本を読み始めたので、その読書メモを。
今回は 2.1 節の「ArrayStack」というデータ構造について。


前置き：「みんなのデータ構造」という書籍について

https://sites.google.com/view/open-data-structures-ja/home より引用。

Open Data Structures は Pat Morin 氏が執筆した、データ構造の入門書です。本プロジェクトでは、この本の和訳を作成し、PDF ファイルおよびそのソースコードを公開しています。

データ構造やアルゴリズムについて学びたいと思っていたので、この本で勉強することにした。
PDF版であれば日本語でもフリーで手に入るが、私はラムダノート社のサイトから紙書籍＋電子書籍版を購入した。

みんなのデータ構造（紙書籍+電子書籍） – 技術書出版と販売のラムダノート

また、書籍内のサンプルコードはC++で書かれているが、C++はわからないのでTypeScriptで写経することにした。

リポジトリ


本題：ArrayStack について

ArrayStack とは

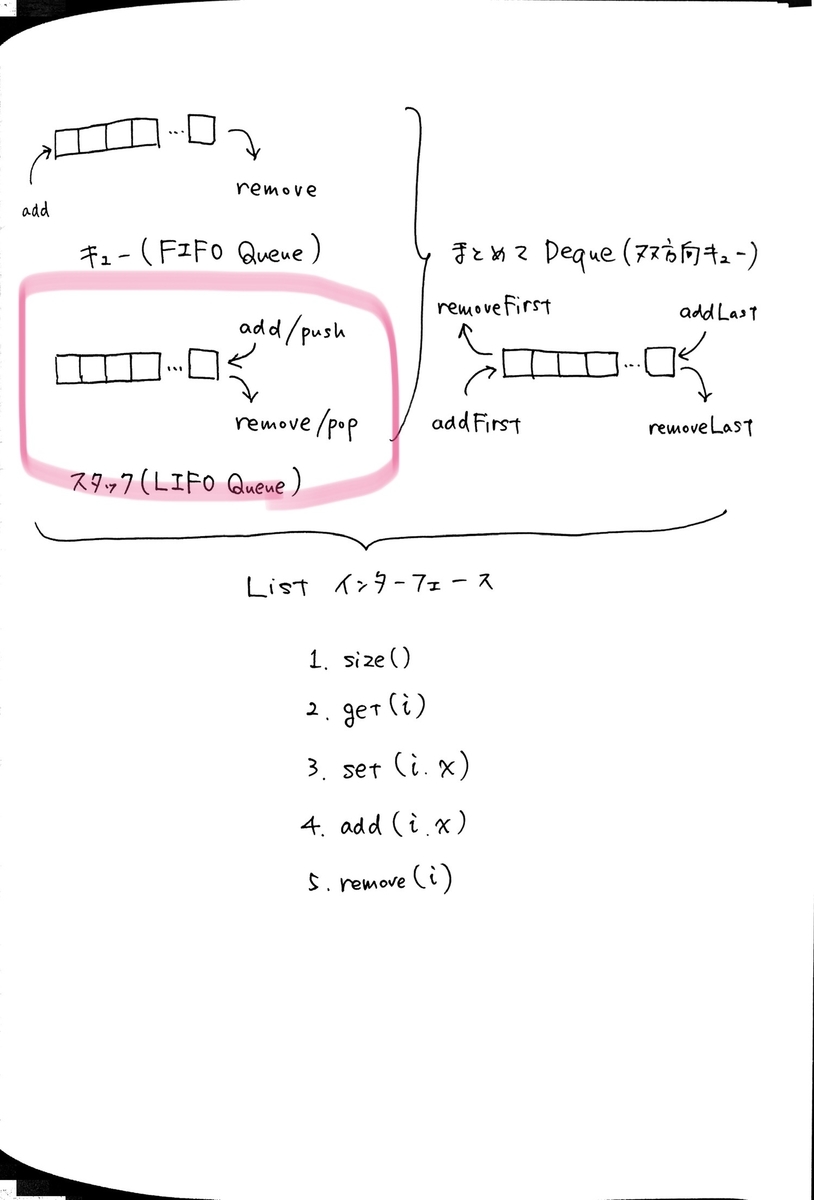
f:id:dackdive:20200106001441j:plain:w320

  • List インターフェースを実装したデータ構造の1つ
  • List インターフェースとは、値の列 x_0, x_1, ... , x_{n-1} とその列に対する以下の操作からなる（1.2.2 より）
    • size(): リストの長さ n を返す
    • get(i): x_i の値を返す
    • set(i, x): x_i の値を x にする
    • add(i, x): x を i 番めとして追加し、 x_i, ... , x_{n-1} を後ろにずらす
    • remove(i): x_i を削除し、 x_{i+1}, ... , x_{n-1} を前にずらす
  • Stack は LIFO Queue とも呼ばれ、最後に追加された要素が次に削除される
    • イメージは「皿を積んだ状態」（積み上げた皿を取るとき、上から順に持っていく）

ArrayStack の実行時間

  • get(i) および set(i, x) の実行時間は O(1)
  • add(i, x) および remove(i) の実行時間は
    • resize() を考慮しなければ O(n - i)
    • resize() を考慮すると O(1 + n - i) ただしこれは償却実行時間

f:id:dackdive:20200106002955p:plain

「償却実行時間」という言葉が出てくるが、これは「1.5 正しさ、時間計算量、空間計算量」の節に定義がある。

償却実行時間が f (n) であるとは、典型的な操作にかかるコストが f (n) を超えないことを意味する。より正確には、 m 個の操作にかかる実行時間を合計しても、 mf (n) を超えないことを意味する。いくつかの操作には f (n) より長い時間がかかるかもしれないが、操作の列全体として考えれば、1 つあたりの実行時間は f (n) という意味だ。

要するに同じ操作を m 回やったときの実行時間から1回あたりの実行時間を考えるという話。


補題2.1 resize() の実行時間について

ここがしばらくわからなかった。

空のArrayStackが作られたあと、 m \geq 1 回の add(i, x) および remove(i) からなる操作の列が順に実行されるとき、 resize() の実行時間は O(m) である。

書籍では

  1. resize() が呼ばれるとき、その前の resize() から add/remove が実行された回数は n/2 -1 以上である
  2. 1を満たすとき、 resize() の実行時間の合計は O(m) である

という2段階で説明しており、また 2 → 1 の順に証明している。
ここでは普通に1から書く。

    1. resize() が呼ばれるとき、その前の resize() から add/remove が実行された回数は n/2 -1 以上である

resize()が呼ばれるのは、add(i, x) 内で呼ばれるケースと remove(i) 内で呼ばれるケースの2通りある。


ケース1: add(i, x) 内で呼ばれる場合

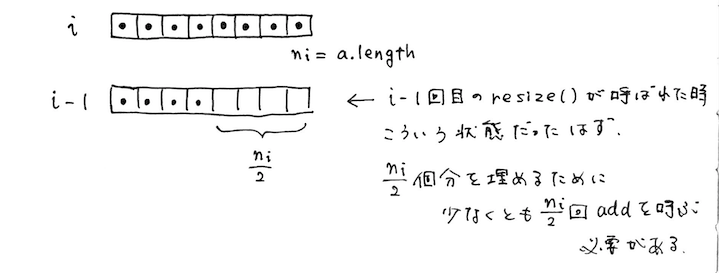
f:id:dackdive:20200106004339p:plain

※書籍に倣って、「◯回めの resize() か」を表す◯に i を使っているが、これは add(i, x) の i とは無関係。ややこしい

この場合は i 回めの時点では配列 a は要素で満たされた状態、 i - 1 回めの時点では配列 a の長さは同じで、要素数は半分。
なので空いている a.length /2 = n_i / 2 分を埋めるのに、少なくとも n_i / 2 回の add() は実行されているはずである。


ケース2: remove(i) 内で呼ばれる場合

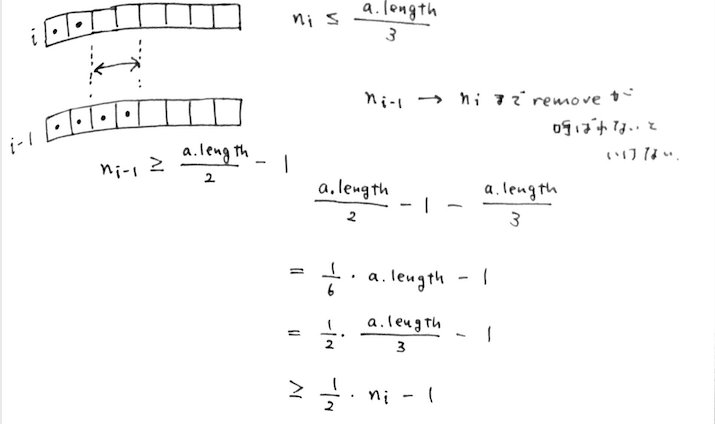
f:id:dackdive:20200106004401p:plain

逆に remove(i) 内で呼ばれる場合、要素数 n_i が配列 a のサイズの 1/3 以下になる場合なので、 n_i <= a.length / 3。
1つ前の i - 1 回めの resize() が実行された直後の状況を考えると、このときは resize() によって配列のサイズの半分の要素数になっているはず。
n_(i-1) = a.length / 2 でもいいが、n = 0 && a.length = 1 という特殊ケースを考えると n_(i-1) >= a.length / 2 - 1 となる。
今度は要素数が n_(i-1) から n_i になるまで remove() が実行されているはずなので、差をとって↑のように式変形すると n_i / 2 - 1 以上であることが示せる。

  • 2．1を満たすとき、 resize() の実行時間の合計は O(m) である

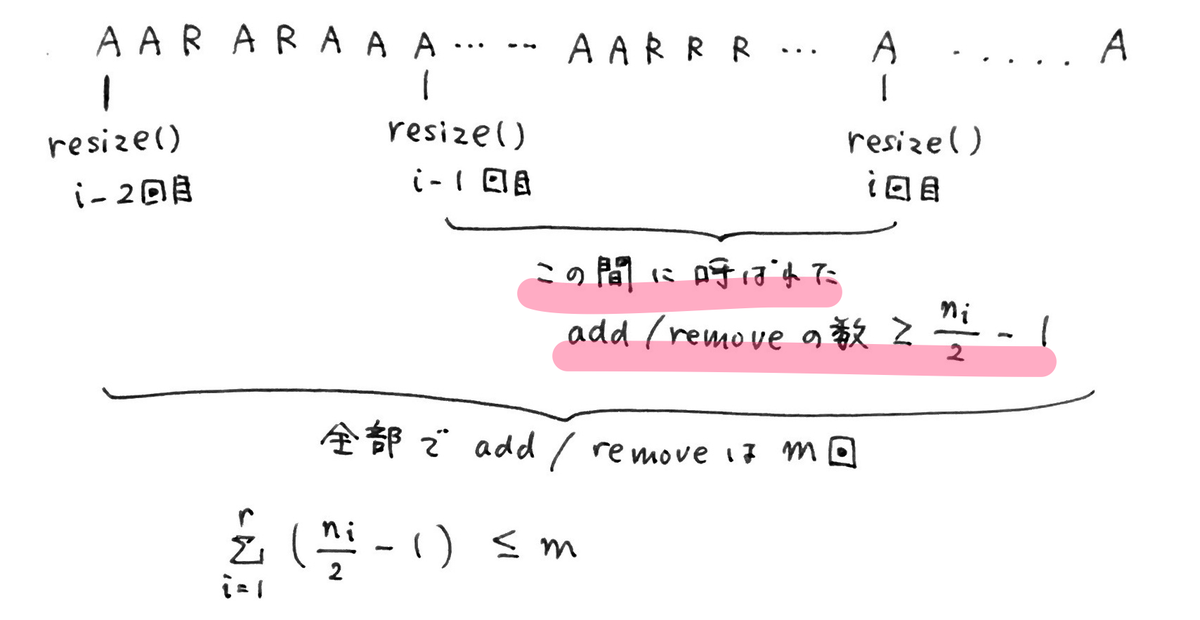
f:id:dackdive:20200106010721p:plain

↑では、add(i, x)を A、 remove(i) を R と表現している。
いま、この AとRをランダムに実行した一連の操作があり、その操作の合計が m 回である。
またこの間に不定期に resize() が実行されており、合計で r 回実行された。

1でわかったのは色をつけた部分で、
「i - 1回めの resize() から i 回めの resize() の間に呼ばれた add/remove の数は >= n_i - 1 である」
ということ。

また、

  (1回めのresize()から2回めのresize()までのadd/removeの数)
+ (2回めのresize()から2回めのresize()までのadd/removeの数)
+ ...
+ (i - 1 回めのresize()からi回めのresize()までのadd/removeの数)
+ ...
+ (r - 1 回めのresize()からr回めのresize()までのadd/removeの数)

<= m

（r 回めの resize() の後にも何回か add/remove が呼ばれている可能性があるため）

で、かつ左辺のそれぞれの項は n_i /2 - 1 よりも大きいと言っているんだから、結局

\displaystyle \sum_{i=1}^r ( \rm {n}_{i} / 2 - 1) \geq m

が示せたことになる。